|
смертность более чем вдвое. В таком случае (14) означает, что взаимное усиление
воздействия больше, чем нелинейное самоусиление. Тогда функция выпукла, и
максимум в задаче (12) достигается либо когда для одного из факторов r
i=fi - фактор нейтрализован, либо когда для одного из них
ri=0 - весь ресурс направлен на борьбу с другими факторами.
В общем случае (12) в каждой вершине многогранника ограничений, задаваемого
уравнением 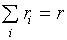 , ,
неравенствами 0£ ri£ fi, для
некоторых m факторов ri=0, для n - m - 1
факторов ri=fi и для одного 0£ ri
£ fi. Если Ф выпукла на гиперплоскости 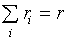
, то максимум достигается в вершине, и получаем ситуацию, согласующуюся с
выдвинутой гипотезой - число влияющих факторов уменьшается до m + 1.
Число m имеет общую для всех вершин оценку сверху. Расположим все f
i в порядке убывания: 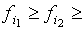
... Положим
r = 0, r1=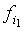 , r2= , r2=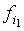 + +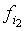 ,., rk= ,., rk=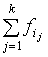 . (15) . (15)
Поскольку предполагается, что r<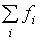
, то для некоторого k=k0<n выполнено неравенство
rk<r<rk+1.
Отсюда следует, что при любом распределении ri (0£
ri£ fi, 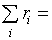
1) число ненулевых ri не меньше, чем k0+1.
Таким образом,
m ³ k0 . (16)
Эта простейшая грубая оценка дает представление о минимально возможном числе
факторов из сильно синергичной группы, воздействие которых на организм в
результате адаптации полностью компенсируется. В итоге адаптации число
действующих факторов уменьшается и происходит сдвиг в сторону
монолимитирования. Напомним, что в качестве условия сильной синергичности
принята выпуклость Ф(f1-r1, f2-r2
, ., fn-rn) на гиперплоскости, задаваемой уравнением 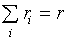
.
Итак, выделены две взаимно дополнительные крайние ситуации: либиховские
системы факторов, для которых в случайном сочетании фенотип-среда (до
адаптации) выполняется принцип Либиха, и синергичные группы факторов, для
которых в случайном сочетании фенотип-среда существенны все факторы, взаимно
усиливающие друг друга. Адаптация к либиховским системам факторов приводит к
полифакториальности, адаптация же к синергичным группам снижает число
действующих факторов, тем самым сдвигая систему в сторону
монофакториальности. Эти выводы подкреплены аналогом простейших базовых
моделей, основанных на представлении о разделении плотностно-зависимых
эффектов и всех остальных действующих факторов. Основной инструмент анализа -
экстремальный принцип Холдейна. Другие упрощения, принятые в моделях и не
связанные с данным разделением, не столь принципиальны; с указанной точки
зрения существует значительный простор для простых обобщений. Более сложная
задача - отказ от основного упрощающего предположения, частичному решению
которой посвящен следующий раздел.
6. Динамика отбора в системах с факторами различных типов
Попытаемся смоделировать результат адаптации с помощью моделей отбора. Идея
подхода уже обсуждалась в предыдущем разделе: вводится множество “адаптивных
возможностей” Ux и рассматриваются оптимальные (по Холдейну)
фенотипы из данного множества. Эта идея в данном разделе несколько
модифицируется: рассматривается множество адаптивных возможностей и отбор на
этом множестве. Так как результаты отбора могут быть описаны с помощью
экстремального принципа, обобщающего принцип Холдейна [8, 33], предлагаемая
модификация может рассматриваться как ближайшее обобщение исходной идеи.
Итак, результаты адаптации моделируются как результаты естественного отбора
на заданном множестве возможностей. Отбор, однако, представляется не в виде
отдельного “действующего фактора”, а как результат динамики численности.
Поэтому первым шагом должно стать описание фазового пространства и
конструкций уравнений этой динамики.
Рассматривается единое пространство возможностей. Оно предполагается компактным.
Точки X характеризуются некоторым набором параметров. Поскольку при
изучении адаптации нас будет особо интересовать распределение адаптационного
ресурса по факторам (ri; i=1,., n), выделим
эту группу параметров. Обозначим вектор с координатами ri
через 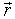 (напомним, (напомним,
что 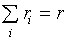 ). Как и выше, ). Как и выше,
принимаем одноресурсную модель. Набор остальных параметров обозначим y.
Распределение особей по пространству X - некоторая неотрицательная мера
m. Предполагается, что m согласована с топологией, т.е. является мерой Радона -
непрерывным линейным функционалом на банаховом пространстве непрерывных функций
C(X).
На C(X) фиксируется топология равномерной сходимости, на
пространстве мер C*(X) - слабая (широкая) топология.
Результат действия функционала m на функцию f (интегрирования)
обозначается как 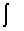
f dm. Произведение меры jm на непрерывную функцию j задает по определению
функционал 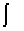
fj dm.
Уравнение, задающее изменение m со временем, записывается так:
¶m(t)/¶t=K(X, m)m, (17)
где K(X, m) - функция, непрерывная по совокупности аргументов
(коэффициент размножения).
Предполагается существование предельной численности N для всех m,
имеющих содержательный смысл, 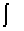
1dm £ N. Сохранение этого неравенства в силу (17) со
временем обеспечивается условием: при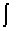
1dm = N коэффициент размножения отрицателен - K(X,
m)<0 (при достижении предельной общей численности количество любых организмов
начинает уменьшаться).
Центральный вопрос в динамике отбора состоит в характеризации всех w-предельных
распределений. Распределение m* называется w-предельным для решения
(17) m(t), если существует такая последовательность ti®
¥, что m(ti)®m*. Основным инструментом при
изучении w-предельных распределений является следующая теорема [8]. Пусть m(
t) - решение (7) с начальным условием m(0)=m0, m* -
какое-нибудь w-предельное распределение для решения: ti®
¥, m(ti)®m*. Рассмотрим последовательность
средних коэффициентов размножения на отрезках [0, ti]:
ki(x)=(1/ti)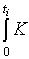 (x, m(t))dt. (18) (x, m(t))dt. (18)
Из нее можно выделить сходящуюся последовательность, так как пространство мер
MN={m çmÎC¥(X), m³0, 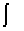 1dm £ N}. (19) 1dm £ N}. (19)
слабо компактно [3]. Пусть k(x) - предел любой такой
подпоследовательности. Тогда k(x) при xÎsupp m
*, k(x)£0 при xÎsupp m0,
т.е. m* составлен из точек (нулевого) максимума k(x)
на носителе начального распределения.
Средние коэффициенты размножения ki и их пределы k
принадлежат замкнутой выпуклой оболочке множества K(., M
N) в C(X). Обозначим эту оболочку Q. Множество
функций компактно. Исследуя свойства точек максимума в X функций k
ÎQ, будем получать информацию о возможных носителях предельных
распределений для решения (7). На этом пути получены теоремы об эффективности
отбора [8, 33], оценки числа точек в носителях предельных распределений [8].
Здесь используется данный прием, чтобы перенести утверждения, полученные для
простейших случаев в предыдущих разделах, на свойства w-предельных (в том числе
стационарных) распределений, складывающихся в ходе отбора. Важным окажется
следующее простое соображение. Пусть все функции K(., m),
(mÎMN) лежат в некотором замкнутом выпуклом
подмножестве C(X). Тогда Q также лежит в этом
подмножестве.
Коэффициент размножения k зависит, конечно, от внешних факторовf
1, f2,., fn. Назовем зависимость k(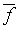
,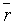 , y, m) , y, m)
либиховской, если
k=y (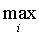 (f (f
i - ri, y, m))
(20)
и при любых y, mÎMN функция k(.
, y, m), монотонно убывающая. Нам потребуется также некоторое усиление
этого условия. Назовем коэффициент размножения k равномерно
либиховским, если существует такая монотонно убывающая функция j(c)
вещественной переменной c, что функция (20) убывает быстрее нее: для
любых y, m, c1<c2 из соответствующих
областей определения
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9
|
